This article needs attention from an expert on the subject. See the talk page for details. WikiProject Mathematics or the Mathematics Portal may be able to help recruit an expert. (January 2010)

It has been suggested that this article or section be merged into Dimension. (Discuss)

It has been suggested that this article or section be merged into Euclidean space. (Discuss)

An n-dimensional space is a topological space whose dimension is n, given by the cardinality of a maximal set of linearly independent elements. An example is n-dimensional Euclidean space (Eⁿ), which describes Euclidean geometry in n dimensions. n-dimensional spaces with large values of n are sometimes called high-dimensional spaces. In linear algebra an n-dimensional space is called a vector space.

Many familiar geometric objects can be generalized to any number of dimensions. The two-dimensional triangle and the three-dimensional tetrahedron are specific instances of the n-dimensional simplex; the circle and the sphere are specific instances of the n-dimensional hypersphere. An n-dimensional manifold is a space that locally is an n-dimensional Euclidean space, but whose global structure may be non-Euclidean. Elliptical (Sⁿ) and hyperbolic spaces (Hⁿ) are n-dimensional spaces with constant positive and negative curvature respectively.

The state of an object with n degrees of freedom can be described as a point in some n-dimensional space; for example, classical mechanics describes the three-dimensional position and momentum of a point particle as a point in 6-dimensional phase space. The numbers that describe a point may represent anything; for this, multivariate statistics and machine learning theory make extensive use of high-dimensional spaces. Fractional and negative dimensions can apply to more general spaces, such as the Hausdorff dimension in topology and Kodaira dimension in algebraic geometry. Infinite-dimensional spaces can be formulated in a meaningful way; an example is the Hilbert space, a concept in quantum mechanics.

Contents [hide] 1 History 2 Applications 3 Properties 4 See also 5 References 6 External links

[edit] History

The abstract notion of coordinates was preceded by the homogeneous coordinates of August Ferdinand Möbius in 1827. The introduction of Cartesian coordinates reduced the three spatial dimensions to a list of three real numbers. Since this list did not have a restriction on its number of members, there existed the possibility of higher-dimensional geometry. Bernhard Riemann, in his 1854 habilitation Über die Hypothesen welche der Geometrie zu Grunde liegen, considered a point to be represented by a list of n numbers 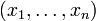without any geometric picture implied. He explained the value of this abstraction thus:^[1]

"Solche Untersuchungen, welche, wie hier ausgeführt, von allgemeinen Begriffen ausgehen, können nur dazu dienen, dass diese Arbeit nicht durch die Beschränktheit der Begriffe gehindert und der Fortschritt im Erkennen des Zusammenhangs der Dinge nicht durch überlieferte Vorurteile gehemmt wird."

Loosely translated:

"Abstract studies such as these allow one to observe relationships without being limited by narrow terms, and prevent traditional prejudices from inhibiting one's progress."

[edit] Applications

Pure and applied mathematics include many abstract sets and applied models with arbitrarily high and infinite dimensions, due to the simple constructions required to construct the necessary spaces. For instance, the configuration space of a rigid body in Euclidean 3-space is the 6-dimensional group of rigid motions E⁺(3), with 3 dimensions for position (translation) and 3 for orientation (rotation); a black-and-white image with 1000 pixels can be viewed as a point in 1000-dimensional space, whose components indicate the darkness of each pixel. This approach allows for generalization of many analysis techniques, and is important in disciplines such as machine learning. Sometimes, dimension reduction techniques are used to deal with very high dimensional data, particularly when the number of dimensions is higher than the number of data points available. In geometric topology, 5 or more-dimensional spaces are considered high due to the nature of the difficulties in the subject that imply dimensions 3 and 4 being the most resistant and therefore most studied.

[edit] Properties

Spaces with a dimension higher than 3 have properties that differ greatly from the intuitions generated by the 3-dimensional space of reality. In particular, as the dimension increases, the volume of an object increases faster. The implications of this include:

• almost all of the volume within a high-dimensional hypersphere lies in a thin shell near its outside. This is important to gaining an understanding of how the chi-squared test works.
• the volume within a high-dimensional hypersphere, relative to a hypercube of the same width, tends to zero as dimensionality tends to infinity, and almost all of the volume of the hypercube is concentrated in its "corners".
• the curse of dimensionality, the intractability of problems in high-dimensional spaces.

An understanding of the derivation of the Shannon limit in coding theory depends on the properties of high-dimensional spaces.

[edit] See also

• Coordinate space
• n-dimensional calculus
• Facet (mathematics)
• Four-vector
• Kissing number problem
• Vector decomposition
• Combinatorial explosion
• Curse of dimensionality
• Dimension theory
• High-dimensional statistics
• Hilbert space
• Minkowski spacetime
• Supporting hyperplane

[edit] References

[edit] External links

• High-dimensional data analysis
• High-dimensional spaces are counterintuitive (in five parts)
• Visualizing Multidimensional Geometry with Parallel Coordinates by Alfred Inselberg
• Other Dimensions of the Universe

[hide][hide]v · d · eDimension Dimensional spaces One · Two · Three · Four · Five · Six · Seven · Eight · n-dimensions · Spacetime · Projective space · Hyperplane Polytopes and Shapes Simplex · Hypercube · Hyperrectangle · Demihypercube · Cross-polytope · n-sphere Concepts and mathematics Cartesian coordinates · Linear algebra · Geometric algebra · Conformal geometry · Reflection · Rotation · Plane of rotation · Space · Fractal dimension · Multiverse Category